Analysis of repeated grooming data by standard fatigue testing makes it possible to predict the likelihood of hair breakage. Using this method Trefor A Evans, Kimun Park, Brian Yang, Murat Kadir, Sascha Herrwerth & Burghard Gruening find considerable benefits from shampoo and conditioner using silicone quaternium-22
The presence of broken fibres can be a major detractor in the quest for beautiful hair. For some, just seeing broken hair fragments in a brush or comb can be a source of worry. This is largely because broken fibres fray and lead to the formation of unsightly split ends, but also fibres no longer align as readily, often reducing the perception of hair smoothness, inducing a degree of frizz, lowering shine and hindering a fluid flowing motion. Consumers therefore worry about breakage and look to product manufacturers for help.
Attempts at resolving this issue begin with a better understanding of the problem and the factors that lead to breakage. Two previous publications[1,2] have focused on modeling hair fibre breakage under fatiguing conditions. Conventional tensile testing of hair generally involves applying a one-time external force or deformation that is sufficient to induce breakage. However, fatiguing involves the repeated application of relatively small stimuli which may be considered more analogous to the rigours associated with everyday grooming. Fundamental single fibre fatigue studies[1] showed an exponential relationship between the magnitude of the applied repeating stress and the tendency for hair breakage. It therefore becomes apparent how a lubricating conditioner treatment that lowers the stresses associated with grooming will consequently produce a reduced tendency for hair breakage.
| Table 1: Shampoo formulations | |||
| Ingredients | Formula A wt% | Formula B wt% | Formula C wt% |
| Water | qs to 100 | qs to 100 | qs to 100 |
| Sodium laureth sulfate | 9.0 | 9.0 | 9.0 |
| Cocamidopropyl betaine | 2.5 | 2.5 | 2.5 |
| Polyquaternium-10 | 0.3 | 0.3 | 0.3 |
| Palmitamidopropyltrimonium chloride | 1.0 | 1.0 | 1.0 |
| Silicone quaternium-22 (65% active) | – | – | 1.54 (1 wt% active) |
| Silicone quat microemulsion (22% active silicone quaternium-16) | – | 4.55 (1 wt% active) | – |
| PEG-200 hydrogenated glyceryl palmate; PEG-7 glyceryl cocoate | 0.9 | 0.9 | 0.9 |
| NaCl | 0.2 | 0.2 | 0.2 |
| Preservative | 0.3 | 0.3 | 0.3 |
| Table 2: Conditioner formulation | |
| Ingredients | Formula D wt% |
| Water | qs to 100 |
| Ceteareth-25 | 0.5 |
| Cetyl alcohol | 5.0 |
| Silicone quaternium-22 (65% active) | |
| Preservative | 0.3 |
A rather dramatic illustration of this benefit can be obtained by performing in vitro repeated grooming experiments on hair tresses, where the number of broken fibres is recorded as a function of the number of grooming strokes. The work described here invokes an analysis approach commonly used in the fatigue testing field to model hair breakage from such experiments. In doing so, this approach provides predictions as to the likelihood for hair breakage under different conditions and shows how shampoos and conditioners involving silicone quaternium-22 provide dramatic anti-breakage benefit.
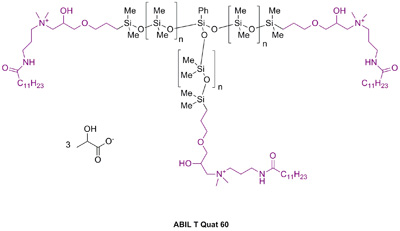
Figure 2: Structure of silicone quaternium-22
Experimental method
Equipment
Repeated combing experiments were performed on a custom built unit shown in figure 1. Detailed descriptions of the equipment together with various experimental details have been given previously.[2] All testing was performed using bleached 8 inch, 3g Caucasian hair tresses obtained from International Hair Importers while grooming involved the head portion of a Goody Purse Style brush. All experiments were performed with the equipment in a climate controlled, walk-in chamber (60% RH, 22°C). Eight tresses were tested per sample.
Tresses were automatically groomed in 1,000 stroke blocks with subsequent counting of broken fibres in the collection trays under each tress. Results were recorded, the trays cleaned and the tresses were cycled through another 1,000 strokes. This process was repeated until a total of 10,000 grooming strokes had been carried out.
Materials and formulations
Silicone quaternium-22 (ABIL T Quat 60) contains a unique T-structured silicone backbone that is end capped with quaternary amine functionality (see figure 2). Thus the molecule carries three cationic charged sites which results in increased substantivity to the hair surface. It can be formulated into both shampoos and conditioners. One particularly attractive feature involves the ability to create effective, clear, conditioning shampoo formulations. Traditional approaches to producing clear conditioning shampoos typically involve the use of silicone microemulsions. However deposition is recognised to be less effective than from their macroemulsion counterparts. For the purposes of this article, the performance of a clear conditioning shampoo based on silicone quaternium-22 will be compared to a formula based on current microemulsion technology. Results and modelling will also be generated using a conditioner formulation based on this same material. Formulations are shown in tables 1 and 2.
| Table 3: Repeated grooming data for bleached Caucasian hair at 60% RH | |||||||||
| # brush strokes | Tress #1 | Tress #2 | Tress #3 | Tress #4 | Tress #5 | Tress #6 | Tress #7 | Tress #8 | Total |
| 1,000 | 37 | 42 | 36 | 52 | 61 | 43 | 58 | 53 | 382 |
| 2,000 | 22 | 9 | 15 | 13 | 15 | 10 | 21 | 19 | 124 |
| 3,000 | 5 | 4 | 7 | 5 | 6 | 5 | 5 | 7 | 44 |
| 4,000 | 4 | 5 | 6 | 4 | 4 | 4 | 4 | 4 | 35 |
| 5,000 | 4 | 3 | 3 | 6 | 4 | 8 | 3 | 4 | 35 |
| 6,000 | 3 | 4 | 5 | 4 | 5 | 6 | 5 | 5 | 37 |
| 7,000 | 3 | 2 | 3 | 3 | 4 | 4 | 4 | 3 | 26 |
| 8,000 | 2 | 3 | 2 | 3 | 3 | 4 | 3 | 3 | 23 |
| 9,000 | 2 | 2 | 2 | 4 | 4 | 3 | 5 | 6 | 28 |
| 10,000 | 2 | 2 | 2 | 2 | 3 | 4 | 4 | 4 | 23 |
| Total | 84 | 76 | 81 | 96 | 109 | 91 | 112 | 108 | 757 |
| Table 4: Grouped Weibull analysis of repeated grooming data for virgin Caucasian hair at 60% RH | ||||||
| Grooming strokes | # failures | Cumulative frequency | Median rank | 1/(1-median rank) | In(In(1/(1-median rank) | Ln (Grooming cycles) |
| 1,000 | 382 | 382 | 0.01909 | 1.0195 | -3.949 | 6.908 |
| 2,000 | 124 | 506 | 0.02528 | 1.0259 | -3.665 | 7.601 |
| 3,000 | 44 | 550 | 0.02748 | 1.0283 | -3.580 | 8.006 |
| 4,000 | 35 | 585 | 0.02923 | 1.0301 | -3.518 | 8.294 |
| 5,000 | 35 | 620 | 0.03098 | 1.0320 | -3.458 | 8.517 |
| 6,000 | 37 | 657 | 0.03283 | 1.0340 | -3.400 | 8.700 |
| 7,000 | 26 | 683 | 0.03413 | 1.0353 | -3.360 | 8.854 |
| 8,000 | 23 | 706 | 0.03528 | 1.0366 | -3.326 | 8.987 |
| 9,000 | 28 | 734 | 0.03668 | 1.0381 | -3.287 | 9.105 |
| 10,000 | 23 | 757 | 0.03783 | 1.0393 | -3.255 | 9.210 |
Results & data analysis
Table 3 shows data for the repeated grooming of hair after washing with the non-conditioning control shampoo (formula A). The most simple, and often a perfectly adequate means of analysis involves comparing the mean number of broken fibres for the different treatments after a given number of grooming strokes. Figure 3 shows such results for the three shampoo formulations after 10,000 grooming strokes. Both shampoo formulations are observed to produce significant benefits, although a considerably greater advantage is seen from formula C (containing silicone quaternium-22 as a conditioning agent). An approximate 60% reduction in breakage is observed upon using this formula.

Figure 3: Average number of broken fibres from repeated grooming of hair tresses treated with various shampoo formulations
However, additional information can be obtained from analysing these results in accordance with fatigue testing principles. In a fatigue test, failure is attributed to the gradual propagation of pre-existing flaws within a material. So in this instance hair breakage ultimately results from flaw propagation induced by repeated forces associated with grooming. The distribution of these flaws is statistical in nature so hair breakage also needs to be treated as a statistical variable. Modelling and characterisation of breakage can be performed by fitting a Weibull statistical distribution to the data.[3] This process is summarised in concise form below, with readers being directed to a previous publication[2] for a more detailed description.
The Weibull distribution is highly flexible and can be used to fit a wide variety of data. This data is subsequently described by evaluation of the two Weibull parameters – the characteristic lifetime and the shape factor. The linear form of the Weibull equation is: In [In (1/1-F(x))] = -β(In x)- β(In α); where F(x) is the probability of the fibre breaking in x cycles; 1-F(x) is the probability of surviving x cycles; a is the characteristic lifetime at which 63.2% of the fibres have broken; and β is the shape factor.

Figure 4: Survival probability plot for grooming of unconditioned bleached hair under the conditions described
Therefore a plot of the double logarithm of the reciprocal of survival probability function versus the logarithm of the number of cycles-to-fail yields the shape parameter from the slope, and the characteristic lifetime from the intercept.
Table 4 shows how the repeated grooming results shown in table 3 can be treated by a grouped Weibull approach.[2,3]
The second column of table 4 contains the total number of broken fibres for all eight tresses as a function of the number of combing cycles (as obtained from table 3). Column 3 then shows the cumulative breakage frequency, while column 4 converts these results into a cumulative distribution function using the well known median rank approach. Columns 5 and 6 show the creation of the double log expression that forms the y axis in the Weibull plot. Meanwhile, column 7 represents the x axis. These calculations (together with the later creation of the survival probability plot) may be set up using an Excel spreadsheet.

Figure 5: Comparison of survival probability plots obtained by grooming bleached hair treated with different shampoo formulas
After evaluation of the two Weibull parameters, it becomes possible to reconstruct the best fitting distribution from which they were derived, and in doing so model the likelihood for survival (or failure) as a function of the number of grooming strokes. The result is termed a survival probability plot[1,2,3] and the outcome of this analysis for the unconditioned bleached hair data is shown in figure 4.
From figure 4 one obviously observes a 100% likelihood of survival when no grooming has been performed, while the survival probability progressively decreases with increasing brushing strokes. Under these conditions it thus becomes possible to predict a 1% likelihood of breakage after only 100 grooming strokes and a 2% failure probability after around 1,000 brushings. While these probabilities may sound low, there are 100,000-150,000 fibres on a typical head, leading to real life breakage predictions which no longer sound so trivial.
It is worth spending a moment to consider typical grooming habits and practices and their relationship to the number of grooming cycles used in these experiments. If we assume that ten grooming strokes are employed each time a consumer brushes their hair and that three such grooming experiences are performed each day, then 1,000 grooming strokes are attained in slightly over a month. Widely different habits and practices obviously exist, but this does not appear to be an unreasonable assumption.

Figure 6: Average number of broken fibres from repeated grooming of hair tresses treated with shampoos and conditioner
Figure 5 now compares results obtained from analysing breakage data for hair tresses treated with the two conditioning shampoo formulations. The anti-breakage benefits are clearly evident, with considerably higher survival probabilities being obtained.
Table 5 summarises the number of repeated brushing strokes predicted by the model to induce a 1% and 2% likelihood of breakage after these treatments.
| Table 5: Number of repeated brushing strokes predicted by the model to induce a 1% and 2% likelihood of breakage after these treatments | ||
| # strokes for 1% breakage probability | # strokes for 2% breakage probability | |
| Formula A | 100 | 1,000 |
| Formula B | 200 | 3,000 |
| Formula C | 2,000 | 25,000 |
So continuing with earlier assumptions regarding habits and practices, it can be seen how formula C retards breakage levels typically seen after a few days of brushing to a level normally seen after a couple of months of grooming. Furthermore breakage levels previously associated with around a month of grooming are not seen until slightly over two years.
The same experiment can also be performed on hair treated with a conditioner formula based on silicone quaternium-22 (see table 2). Breakage results and the subsequent survival probability plots are shown in figures 6 and 7.
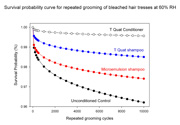
Figure 7: Comparison of survival probability plots obtained by grooming bleached hair treated with shampoos and conditioner formula
The conditioner treatment is observed to retard breakage further. Such low levels of breakage are obtained that it becomes necessary to trust the model beyond the realm of the experimental data for similar performance comparisons to be obtained. However, with this caveat, prediction suggests that 15,000 brushing strokes would be required to induce a 1% likelihood of breakage, while 140,000 strokes would be needed for 2% failure probability.
Treating repeated grooming data by standard fatigue testing analyses allows for the modelling of hair breakage under conditions that appear relevant to consumer habits and practices. The analysis treats breakage as a statistical variable and thus produces a novel means of communication, where it becomes possible to predict the likelihood of hair breakage. The results reflect the considerable benefits obtained by formulas involving silicone quaternium-22.
Authors
Trefor A Evans & Kimun Park, TRI-Princeton, Princeton, NJ 08540, US
Brian Yang & Murat Kadir, Evonik Industries, Hopewell, VA 23860, US
Sascha Herrwerth & Burghard Gruening, Evonik Industries, Essen, Germany
Contact
Trefor Evans
principal scientist, TRI-Princeton, US
tel +609 430 4834
email tevans@triprinceton.org
References
1. Evans TA, A statistical analysis of hair breakage, J Soc Cosmet Chem, 60, 599-616 (2009)
2. Evans TA & Park K, A statistical analysis of hair breakage, Part II - Repeated grooming Experiments, Accepted for publication (J Soc Cosmet Chem)
3. Dodson B, The Weibull Analysis Handbook, American Society for Quality Press, 2nd Edition
